The general equation of a straight line is y = mx + c, where m is the slope of the line and c is the y-intercept. It is the most common form of the equation of a straight line that is used in geometry. The equation of a straight line can be written in different forms such as point-slope form, slope-intercept form, intercept form, standard form, etc. A straight line is a two-dimensional geometrical entity that extends on both ends till infinity.
In this article, we will explore the concept of the equation of a straight line in different forms. Try your hands at solving a few interesting examples and questions for a better understanding of the concept.
| 1. | What is the Equation of Straight Line? |
| 2. | Equation of Straight Line Formulas |
| 3. | Forms of Equation of a Straight Line |
| 4. | Equation of Straight Line on Graph |
| 5. | FAQs on Equation of Straight Line |
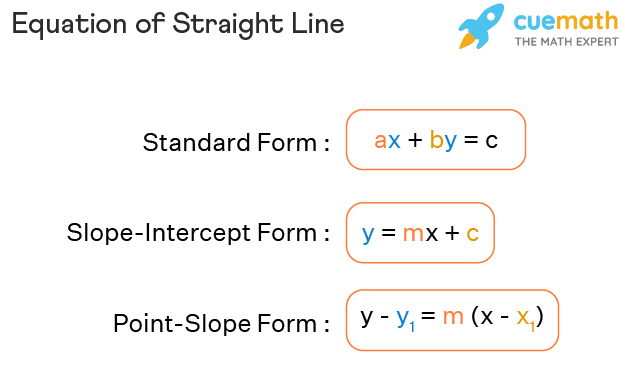
The equation of a straight line is an linear equation in two variables (usually x and y) and is satisfied by every point on the line. i.e. it is a mathematical equation that gives the relation between the coordinate points lying on that straight line. It can be written in different forms and tells the slope, x-intercept, and y-intercept of the line. It also can be used to find the points on the line. Mostly, the equation of a straight line is found by using point-slope form, slope-intercept form, two-point form, standard form, etc. Let us go through the formula for the equation of a straight line.
The most common formulas to find equation of straight line are mentioned below.

The equation of straight line formula varies depending on what information is available about the line like slope, intercepts, etc. Note that the slope of a line with two points (x1, y1) and (x2, y2) is calculated by the formula m = (y2 - y1)/(x2 - x1). Here are different straight line formulas.
| Different Forms of Straight Lines | Equation of Straight Line |
|---|---|
| Two Point-Form (Given two points (x1, y1) and (x2, y2) on the line) | y - y1 = (y2 - y1)/(x2 - x1) (x - x1) |
| Point-Slope Form (Given slope m and point (x1, y1)) | y - y1 = m (x - x1) |
| Slope - Intercept Form (Given slope m and y-intercept (0, c)) | y = mx + c |
| Intercept Form (Given the intercepts a and b) | x/a + y/b = 1 |
| Normal Form (Given θ = the angle made by the normal with positive direction of x-axis and p = distance of line from origin) | x cos θ + y sin θ = p |
| General/Standard Form of a Line | ax + by = c |
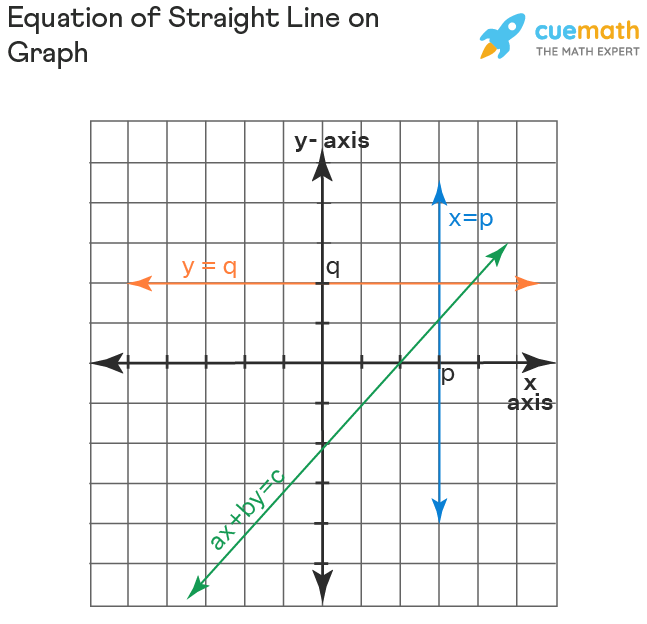
| Equation of a vertical line with some point (a, b) on it | x = a |
| Equation of a horizontal line with some point (a, b) on it | y = b |
We will study each of these in detail in the section below.
The equation of a straight line usually involves slope. Suppose a line l makes an angle of θ with a positive direction of the x-axis, the angle θ is called the inclination of the line and tan θ is called the slope of the line. Note that x-axis has a slope 0. In fact, all lines parallel to the x-axis have a slope of 0. Also, the slope of all the lines parallel to y-axis including the y-axis is not defined.
Now, Let us go through different forms of equations of a straight line.
The equation of a straight line whose slope is m and which passes through a point (x1, y1) is found using the point-slope form. The equation of the point-slope form is:
y - y1 = m (x - x1), where (x, y) is an arbitrary point on the line.
Let us see how to find the point-slope form. We will derive this formula using the equation for the slope of a line. Let us consider a line whose slope is m. Let us assume that (x1, y1) is a known point on the line. Let (x, y) be any other random point on the line whose coordinates are not known. We know that the equation for the slope of a line is:
Slope = Difference in y-coordinates/Difference in x-coordinates
Multiplying both sides by (x - x1),
This can be written as,
Hence the point-slope form of the equation of a straight line is proved.
Consider a line with two points (x1, y1) and (x2, y2) on it. Then its slope can be calculated by the formula m = (y2 - y1)/(x2 - x1). Substituting this in the above point-slope form, we get the two point form as y - y1 = (y2 - y1)/(x2 - x1) (x - x1).
Now, suppose a line is given to you with its slope m and its y-intercept. Say, a line intersects the y-axis at the point (0, c). Using the point-slope form we have y - c = m (x - 0) ⇒ y = mx + c, where c is the y-intercept. This is called the slope-intercept form of a line.
Note: If d is the x-intercept, then the slope-intercept form of the equation of the line is y = m(x - d).
If (a, 0) and (0, b) are the x and y-intercepts of a line respectively. Then its slope is, m = (b - 0)/(0 - a) = -b /a. Then its equation using the point-slope form is:
Multiplying both sides by a
Dividing both sides by ab,
The standard form of a straight line is given by ax + by = c, where a, b, c are real numbers. We can consider any form of a line into standard form. Let us consider an example to transform the equation y = 2x - 1 in the standard form. Subtract 2x from both sides of the equation, we have
y - 2x = 2x - 1 - 2x
So, we obtain the standard form of the equation of the line as 2x - y = 1.
The graph of a linear equation in one variable x forms a vertical line parallel to the y-axis and the graph of the equation of a straight line in one variable y is a horizontal line parallel to the x-axis The graph of a linear equation in two variables x and y forms a straight line with some slope.
If a straight line is increasing from left to right, its slope is positive. If it is decreasing, its slope is negative.
Important Notes on Equation of Straight Line:
☛Related Topics:
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Example 1: Find the equation of a straight line that passes through the points (1, 3) and (-2, 4). Write the equation in standard form. Solution: To determine the equation of the line, we will use the formula point-slope form. For this, we first need to find the slope of the line. Slope = (4-3)/(-2-1) = -1/3 Therefore, the equation of the line passing through (1, 3) and (-2, 4) is y - 4 = (-1/3) (x + 2) ⇒ y - 4 = -x/3 - 2/3 ⇒ y + x/3 = 4 - 2/3 ⇒ x + 3y = 10 Answer: The required equation is x + 3y = 10.
Example 2: The cost of a notebook is $5 more than twice the cost of a pen. Represent the situation as an equation of a straight line. Solution: Assume the cost of pen = $x and the cost of notebook = $y. Then, according to the question, we have y = 2x + 5 which is the equation of a straight line. Answer: y = 2x + 5
Example 3: The equation of a straight line is given by 3x - 4y = 12. Convert this into the intercept form and hence find the intercepts. Solution: The equation of given line is: 3x - 4y = 12 Dividing both sides by 12, 3x/12 - 4y/12 = 12/12 x/4 + y/(-3) = 1 This is in the intercept form x/a + y/b = 1. Hence, the intercepts are (a, 0) = (4, 0) and (0, b)= (0, -3). Answer: x/4 + y/(-3) = 1; Intercepts: (4, 0) and (0, -3).
View Answer >
Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts